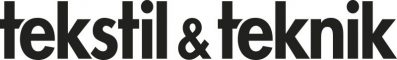Tekstil Teknik Dergisi Tekstil Haberleri, Tekstil Sektörü, Tekstil Teknik
Related Articles
Main Impregnating Systems Using ml/kg
Leonardus Janssen, Consultant of Pulcra Kimya A.Ş.
Erdem Genç, Pretreatment Technical Manager of Pulcra Kimya A.Ş.
Erkan Döner, Regional Manager of Ege-Pulcra Kimya A.Ş.
In the late 80’s and beginning 90’s, the maximum add-on in textile impregnating systems for bleaching and scouring starts one ́s triumph. A variety of different systems were offered by the textile manufactures. Typical of those units was a high add-on off more than 100% combined with a low volume of the impregnating unit. All these units were dosing in [ml/ kg] but using different systems for applying the wanted chemicals on the fabric.
An example of some of those units is visible in Fig. 1. Please note that the depictured sketches are not at all copies of existing units, they are just imitating some working principles. (Fig. 1)
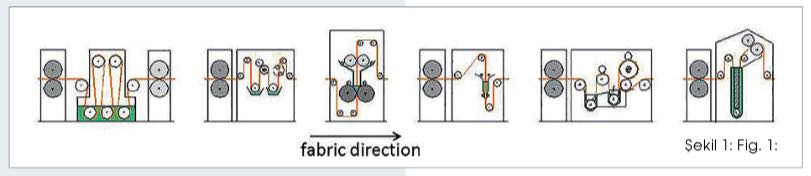
To understand the working principles and the impact on the processed fabric we have to focus on 2 items, the mechanical set-up of the unit and the dosing method used for the impregnating unit.
Both points are completely separated and do not intermingle. The mechanical set-up will be responsible for all parameters once a unit is in equilibrium, whereas the dosing should be evaluated more in view of reliability and a correct and easy handling.
The mechanical set-up of an impregnating unit
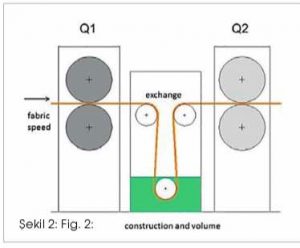Strictly considered we can reduce an impregnating system in a simple drawing as shown in fig 2 where 4 parameters are defining everything what is happening in an impregnating system. The properties of the fabric (at a defined speed, temperature and recipe) together with the water squeezer (Q1) and the construction of the impregnating part will define the exchange. The chemical squeezer (Q2) will define the amount of liquid on the fabric. (Fig 2)
Measuring the parameter involved (chapter 3) and applying them in the formulas given in this paper will give a detailed view of what is physically happening in an impregnating system.
Most of the abbreviations used in here are the following:
m in [kg/min] amount of fabric passing per minute (speed*weight)
t in [min] time
R in [ml/kg] the recipe (of H2O2)
Q1 in [l/kg] the amount of water on the fabric before entering the impregnating system
Q2 in [l/kg] the amount of liquid on the fabric leaving the impregnating system
∆Q in [l/kg] the application difference (Q2- Q1)
f the exchange factor, the amount of water exchanged by the impregnating liquid during impregnating as a numeric value between 0,0 and 1,0
V in [l] the volume of the impregnating unit: total amount of liquid, including mixing vessel and piping.
Epu in [l/kg] effective pick-up (Epu =Q1*f+∆Q where ∆Q=Q2-Q1)
Ct in [ml/l] the concentration in the impregnating unit at a time t
C∞ in [ml/l] the concentration in the impregnating unit at equilibrium (time t=∞)
C0 in [ml/l] the concentration in the impregnating when applying new parameter (start of a new production, change of fabric etc..) for t = 0 CF in [ml/l] the concentration of the feeding liquid.
(CF is the concentration of the sum of water and chemicals leading to the impregnating unit. Not to confuse with the amount of the feeding liquid (which is identical to the add-on).
The squeezing values, respectively application amounts of the liquid on the fabric will have the unit [l/kg]. It is known that the common term for squeezing values is % and very often this nomination will still be used for simple explanations but to avoid mistakes in the formulas used in this paper we will have to use the correct unit in [l/kg].
Characteristics in view of squeezing behaviour and exchange
Every fabric will have its own characteristics in view of squeezing behaviour and exchange. The combined action of fabric, speed, applied recipe and impregnating unit will result in a specific “equilibrium” and “responding time”.
The equilibrium is called the situation where an impregnating system is reaching a final and steady concentration in the impregnating liquid whereas all other parameter as fabric, squeezing, speed etc. remains unchanged.
Of course there will be minor variations in the concentration, but these variations are negligible and normal.
Only when substantial changes are happening, as e.g. pressure loss in the squeezing, different fabrics in view of exchange of fabric, dosing pump failure etc… variation in the impregnating concentration can be observed.
The responding time is defined as the time needed for an impregnating unit to find again to an equilibrium in case of a not adapted concentration in the impregnating bath, as e.g. the start of a unit, changes in the water and/or chemical squeezer or a drastically change in fabric quality.
The equilibrium
The concentration in an impregnating unit, depending on the time, can be expressed by the formula:
Where Ct is the concentration of the impregnating liquid at a time = t and C0 is the concentration of the impregnating liquid at a time = 0. t will have the unit [min].
The concentration of an impregnating unit in equilibrium is definitely reached for t = ∞ . The above formula for t=∞ becomes:
An impregnating with a dosing in [ml/kg] will always find its equilibrium at a concentration defined by the recipe divided by the value of the effective pick-up. Example:
Recipe with 30 [ml/kg] H2O2, Q1 with 70%, Q2 with 95% and f is 0,7
Epu = 0,7*0,7+(0,95 – 0,70) = 0,74 [l/kg] R = 30 [ml/kg] C∞ = 30/0.74 = 40,5 [ml/l] H2O2
Recipe with 30 [ml/kg] H2O2, Q1 with 70%,, Q2 with 110% and F is 0,6
Epu = 0,7*0,6+(1,10 – 0,70) = 0,82 (l/kg) R = 30 [ml/kg] C∞ = 30/0.82 = 36.6 [ml/l] H2O2
Hence, the lower the Epu the higher the difference will be between the value in [ml/kg] of the recipe and the value of the concentration in equilibrium in [ml/l].
The responding time
The responding time and the time to reach a “safe” concentration
Every change of parameter will have an impact on the change of concentration in the impregnating unit. As a consequence, after the change of one or more parameters, the impregnating unit will be on the search for a new equilibrium.
The time necessary to reach a new equilibrium is called the responding time and is based on a time t=∞.
Waiting or calculating the time t=∞ for reaching the concentration C∞ is not possible and only used in the above formulas. Knowing that we always will have some fluctuations in the concentration of the impregnating bath we will use a bandwidth above and below the equilibrium. As such we can calculate with a more realistic time for reaching a “safe” concentration in the impregnating unit.
The responding time can be calculated by the left formula of the equilibrium.
Ct is defining the concentration of the impregnating liquid depending on the time t. For every value of Ct we will have a defined value for t and of course inverse, every time t is related to a concentration Ct.
The relation between t and Ct is given with formula on the right:
where
t = time from C0 to Ct
C0 = concentration at the start
Ct = concentration at the time t
C∞ = expected equilibrium (R/Epu)
V = volume of the compartment
Epu = effective pick-up (Q1*f+∆Q)
m = weight of fabric/min
Further in this paper we will explain how to get hold of most of the important parameters when processing a certain fabric. Once we know these parameters, we will be able to calculate the time which is necessary for the impregnating system to strive for a defined concentration.
At this point it is easy to calculate the “responding time” of the unit to match with a safe concentration ± 5 or ± 10 % of the expected equilibrium.
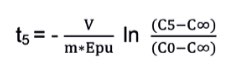
C5 = C∞ * 0,95 if the starting concentration is lower than the expected equilibrium
C5 = C∞ * 1,05 if the starting concentration is higher than the expected equilibrium (for C10 respectively 0,90 and 1,10)
Example:
A production is starting with fabric A, after 200 minutes this production is interrupted for another fabric B and after 400 minutes the production is again on fabric A. Both fabrics will have a recipe of 35 [ml/kg] Processing speed: 80 m/min
The liquid content of the impregnating unit is measured with 250 liter. (Fig 3)
The parameters of fabric A:
Weight: 275 [g/m] or 0,275 [kg/m]
Q1: 70% or 0,70 [l/kg]
Q2: 110% or 1,10 [l/kg]
f: 0,55
The parameter of fabric B:
Weight: 250 [g/m] or 0,250 [kg/m]
Q1: 65% or 0,65 [l/kg]
Q2: 100% or 1,00 [l/kg]
f: 0,45
